[Algorithm] Dynamic Programming-1(Definition, Fibonacci)

Dynamic programming is a method for solving large problems by breaking them down into smaller subproblems. This way, you avoid having to repeat the solutions to each subproblem multiple times, allowing you to solve the overall problem much faster.

This approach typically works well when a problem has two characteristics:

-Optimal substructure

Optimal substructure means that the optimal solution to the overall problem can be constructed from the optimal solutions to its subproblems

-Overlapping subproblems

Overlapping subproblems means that the same subproblems recur many times.

Let's see the fibonacci sequence.

When solving n'th term of sequence, recursion is very easy way.

def fibonacci(n):
    if n<=2:
      return 1
    else:
      return fibonacci(n-1) + fibonacci(n-2)

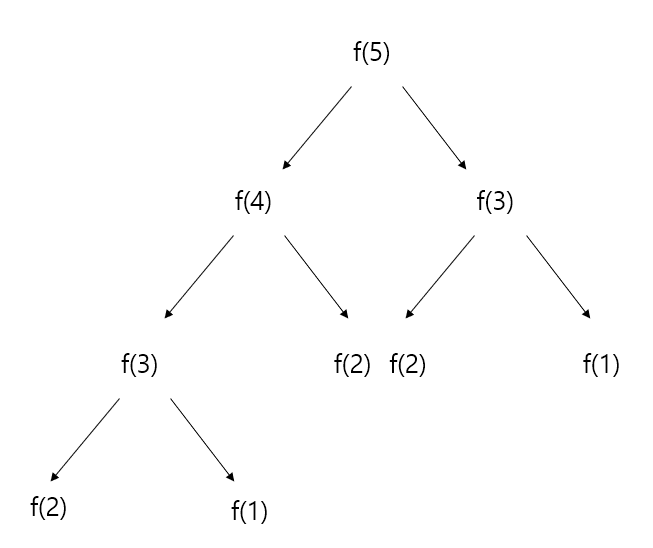
In this code, there are too many calculation. For example, fibonacci(5)

When you compute fibonacci(5), you go through the process as described above. From the diagram, you can see that operations for f(1), f(2), and f(3) are duplicated. If you store the results of f(1), f(2), f(3) somewhere, you won't need to perform these operations again.

Dynamic Programming is a way of solving complex problems by breaking them down into simpler subproblems, solving them, and then combining them to solve the final problem. If the same subproblem appears, you can use the answer you've previously calculated and stored. This is similar to the Divide and Conquer approach, but the difference is that in Divide and Conquer, subproblems do not overlap.

Memoization is a method where you pre-calculate and store results to reduce repeated computations when the same problem needs to be solved repeatedly. Dynamic programming can efficiently solve overlapping subproblems using memoization.

There are two approaches to using Dynamic Programming for solving the Fibonacci sequence: the Top-down approach and the Bottom-up approach. Let's divide the method of obtaining fibo(n) into two using the Fibonacci sequence as an example.

1. Top-down Approach

Divide a large problem into smaller (subproblems).

Solve the smaller problems (subproblems).

Combine the solutions to the smaller problems to solve the final problem.

If we take the Fibonacci sequence as an example, we go through the following process:

Divide a large problem into smaller (subproblems).

Split the problem into fibonacci(n-1) and fibonacci(n-2).

Solve the smaller problems (subproblems).

Calculate fibonacci(n-1) and fibonacci(n-2). If these values have already been calculated, use the stored values. If not, save these in a memoization array.

Combine the solutions to the smaller problems to solve the final problem.

Add fibonacci(n-1) and fibonacci(n-2) to calculate fibonacci(n).

Implementing this in Python language is as follows.

# Top-down

dp = [0]*100  # memoization array to store answers to subproblems

def fibo(n):
    if n <= 1:
        return n
    else:
        if dp[n] > 0:  # if answer to this problem exists
            return dp[n]
        dp[n] = fibo(n-1) + fibo(n-2)
        return dp[n]

If you implement it in a Top-down manner like this, you can't fully leverage the benefits of memoization. While the number of operations decreases, making it more efficient than the original method, it is still inefficient due to the overhead caused by recursive function calls.

2. Bottom-up Approach

The Bottom-up approach is a method where we solve smaller problems first and then combine them to solve larger problems.

Solve smaller problems first.

Use the solutions of the smaller problems to solve the larger problem.

Repeat this process to solve the final problem.

If we take the Fibonacci sequence as an example, we would follow these steps:

Solve smaller problems first.

Calculate dp[i-1], dp[i-2] for fibo(i-1), fibo(i-2).

Use the solutions of the smaller problems to solve the larger problem.

Use dp[i-1] + dp[i-2] to calculate dp[i].

Repeat this process to solve the final problem.

Repeat this process to calculate dp[n].

Implementing this in Python language is as follows.

# Bottom-up

dp = [0]*100  # memoization array to store answers to subproblems

def fibo(n):
    dp[0] = 0
    dp[1] = 1
    for i in range(2, n+1):  # repeat from 2 to n
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

If the Fibonacci sequence is solved in the bottom-up method using the memoization array, there is no overhead due to the call of the recursive function, and the number of operations is reduced, making it efficient.